Le système de numérotation
Un système de numérotation est une représentation séquentielle d'un ensemble de nombres, précise et structurée, qui s'effectue à l'aide d'un ensemble de symboles appelé « chiffres ». Nous aussi le définir comme une façon d'énoncer ou d'écrire des nombres sauf qu'il existe plusieurs systèmes de numérotation tels que : le système décimal le plus connu (C'est celui qu'on utilise tous les jours), le système binaire, le système hexadécimal, etc. Ainsi, chaque système repose sur une « fondation » qui définit le nombre de symboles utilisés.
Prenons l'exemple du système le plus connu : le système décimal. Ce système repose sur 10 chiffres, allant de 0 à 9, pour constituer un ensemble infini de nombres.
Dans le monde de l'electronique, nous retrouvons principalement 4 systèmes de numérotation, à citer:
- Le système décimal: est le plus utilisé dans la vie courante. Il se base sur dix chiffres, allant de 0 à 9. On l'appelle aussi système de numérotation à base de 10.
- Le système binaire: c'est le système le plus élémentaire dans le domaine de l'électronique. Il se base sur deux états, ON et OFF, qui équivalent respectivement à 0 et 1 (ou, dans certains systèmes électroniques, à l'état bloqué et à l'état passant).
- Le système octal: on l'appelle aussi « système à base 8 ». Ce système utilise les chiffres de 0 à 7. Chaque position d'un chiffre représente une puissance de 8.
Dans le système informatique, chaque caractère est représenté par un nombre défini de chiffres, appelé octet ou digit. - Le système hexadécimal: Ce système de numérotation est basé sur 16 au lieu de 10. Il utilise une combinaison de chiffres (de 0 à 9) et de lettres (de A à F) pour représenter les valeurs de 10 à 15.
Codage, Décodage, Transcodage ?
Le codage dans les systèmes de numérotation consiste à convertir un nombre exprimé dans un système de numérotation en base 10 dans un autre système de numérotation. La conversion d'un nombre décimal vers un nombre binaire, octal ou hexadécimal s'appelle également codage. La conversion inverse, appelée décodage, consiste à retrouver l'équivalent en décimal d'un nombre exprimé dans un système autre que le système décimal.

La conversion d'un système de base B1 vers un système de base B2 telle que B1 et B2 ne sont pas des systèmes de base 10 s'appelle le transcodage. Le tableau ci-dessous récapitule les 16 premiers entiers dans les différents systèmes de numérotation:
| Décimal | Binaire | Octal | Hexadécimal |
| 0 | 0000 | 00 | 0 |
| 1 | 0001 | 01 | 1 |
| 2 | 0010 | 02 | 2 |
| 3 | 0011 | 03 | 3 |
| 4 | 0100 | 04 | 4 |
| 5 | 0101 | 05 | 5 |
| 6 | 0110 | 06 | 6 |
| 7 | 0111 | 07 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Cette conversion entre les différentes bases numériques; décimal, binaire, octal, hexadécimal, ... appelée aussi codage, décodage et transcodage se fait généralement à travers des algorithmes qui décomposent les nombres en parties entières et les fractionnaires en utilisant des divisions successives. Ce mécanisme repose essentiellement sur des opérations de divisions euclidiennes qui permettent d'obtenir des quotients et des restes pour constituer le résultat demandé.
Le transcodage
Le processus de conversion d'un système de numérotation à un autre s'appelle le transcodage. Ce processus de conversion est valable quel que soit le système de numérotation d'origine ou de destination. Pour simplifier la conversion, il est possible de transiter par le système de numérotation décimal si le système de départ ou de destination n'est pas le système décimal.
Par exemple, pour convertir la valeur 3E du système hexadécimal vers le système octal, il faut d'abord convertir la valeur 3E dans le système décimal, soit la valeur de 62, puis la convertir dans le système octal pour obtenir la valeur de 76.
Ci-dessous comment nous procédons :
- \( 3E = 3 * 16 + 14 = 48 + 14 = 62 \)
- \( 62/8 = 7 \) et il reste 6 ce qui donne 76 en octal (l'image ci-dessous détaille ce calcul)

Comment effectuer un transcodage ?
Pour convertir un nombre d'un système décimal à un autre, il est demandé d'abord de l'écrire dans le système décimal en base 10, puis dans le système de numérotation demandé (comme expliqué ci-dessous). La complexité de cette conversion réside dans le passage du système en base 10 vers le système de numérotation demandé. Pour cela, il faut effectuer des divisions euclidiennes par d (où d est la base du système de destination) jusqu'à ce que le reste de la division euclidienne soit 0. Le reste de toutes les divisions à l'exception de la valeur 0 finale, de bas vers le haut, est donc le nombre dans le système recherché.
En expression mathématique, la division euclédienne s'écrit comme suit : \( a = b \times n + r\), avec a par b, nous devons obtenir un résultat n avec un reste r. Ci-dessous un exemple de conversion de la valeur décimale 9 en binaire qui démontre la mise en place de la division euclidienne répétitive:
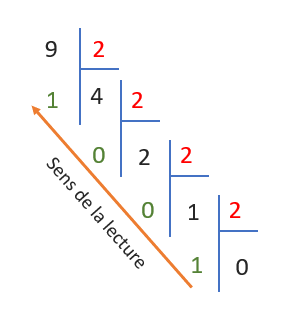 Ainsi, le 9 exprimé en système de numérotation décimal équivaut à 1001 en base binaire (système en base de 2).
Ainsi, le 9 exprimé en système de numérotation décimal équivaut à 1001 en base binaire (système en base de 2).
Les opérations et les opérateurs
Pour chaque système de numérotation, un ensemble d'opérations a été établi pour chaque système de numérotation, binaire, décimal, hexadécimal ou octal. Ces opérations sont basées sur des notions essentielles en mathématiques et en informatique et permettent la possibilité de résoudre des problèmes simples, tels que des calculs arithmétiques de base, mais aussi des équations plus complexes. En utilisant ces opérations dans divers systèmes, il est possible de gérer efficacement les données, ce qui facilite la compréhension et le traitement des informations, tels que la programmation, l'algorithmique et l'analyse de données.
Les opérateurs
Pour la résolution mathématique ou logique, nous pouvons citer les cinq opérations suivantes qui nous permettent d'effectuer l'ensemble des actions mathématiques ou logiques sur des données ou des nombres tels que:
- Addition: permet de calculer la somme de deux ou plusieurs nombres de données. Le symbole de cette opération est le caractère plus (+)
- Soustraction: elle permet de retirer une un nombre ou une quantité d'un autre. Son symbole est noté par le signe moins (−)
- Multiplication: pour ajouter un nombre ou une donnée à elle-même plusieurs fois, la multiplication nous permet de le faire. Elle est notée par le signe multiplié (×) dans la plupart des cas et dans certains cas par le point (·)
- Division: Pour partager une quantité, un nombre ou une donnée sur un ensemble de part égale, la division nous le permet de le faire. Le symbole de la division est le signe divisé (÷) ou la barre de fraction (/) en fonction des ouvrages (pas de préférence mathématique par rapport à cette notation)
- Modulus, soit le reste de la division euclidienne: est souvent noté avec le symbole (%), elle nous permet d'obtenir le reste de la division euclidienne entre deux nombres donnés.
Les opérateurs
Dans une perspective d'analyse numériques et relationnels, logiques ou même arithmétiques, plusieurs opérateurs ont été définis ou réservés pour effectuer des calculs élémentaires, comparer des valeurs, effectuer des combinaisons logiques, manipuler des données, etc.
Nous pouvons citer quelques un tels que:
- Opérateurs relationnels: égal, différent, supérieur ou égal, inférieur ou égal, strictement supérieur, strictement inférieur.
- Opérateurs logiques: ET, OU, NON
- Opérateurs d'affectation: affection simple, affection d'addition, affection de soustraction, affectation de multiplication, affection de division, ...
- Opérateur élémentaire: ET, OU, NON, décalage à gauche, décalage à droite, ...