Le théorème de Millman

Le théorème de Millman, proposé par le physicien Jacob Millman, est l'un des fondamentaux de l'électronique et un outil essentiel pour l'analyse des circuits électriques. Il s'applique à un circuit constitué de plusieurs branches parallèles connectées entre-elles pour déterminer la valeur de la tension V à un point choisi.

Principe du théorème de Millman

Ce théorème permet de déterminer la valeur de la tension dans un nœud n la valeur V si nous connaissons les différentes valeurs V_i de la différence de potentiel de chaque nœud d'interconnexion de chacune des branches (soit dans le schéma ci-dessous la tension V_i = U_Ei + E_Ri). Il en résulte que chaque branche est modélisée sous forme d'une source de tension connecté en série avec un dipôle linéaire; soit l'équivalent d'une résistance R_i. Si la branche ne dispose pas de générateur de tension ou toute autre source d'alimentation électrique, elle se réduit donc à sa valeur résistive.

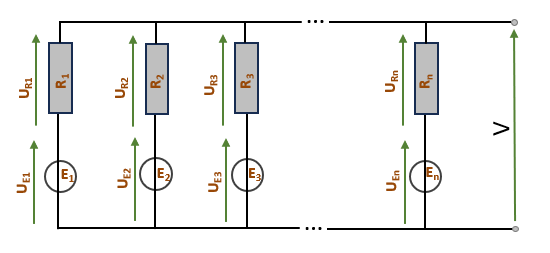
Ainsi, ce théorème permet d'écrire le potentiel d'un nœud donné en fonction des autres valeurs de la différence de potentiel dans un circuit électrique donné. La formule mathématique proposée par Jacob Millman pour déterminer la valeur V au nœud est la suivante:

\[ V = \frac{\sum{\frac{V_{i}}{R_{i}} } }{\sum{\frac{1}{R_{i}}}} \]

Cette théorie reste valable pour les courants alternatifs sinusoïdaux comme pour les courants continus.

Un cas pratique

Prenons maintenant le schéma électrique ci-dessous comme un premier exemple:

En appliquant ainsi le théorème de Millman, la valeur au point potentiel V s'écrit comme suit:

\[ V = \frac{(V_{1}/R_{1})+(V_{2}/R_{2})+(V_{3}/R_{3})+(V_{4}/R_{4})+(V_{5}/R_{5})}{(1/R_{1})+(1/R_{2})+(1/R_{3})+(1/R_{4})+(1/R_{5})} \]

Exemple d'application

Ce théorème s'applique à tout circuit électrique composé de plusieurs branches montées en parallèle, chaque branche disposant de sa propre source de tension et d'au moins un composant électrique linéaire passif, comme une résistance. Les applications les plus courantes de ce théorème sont les convertisseurs de tension, les mélangeurs de tensions, les circuits à ampli AOP (Amplification Opérationel) et certains types de filtres passif RC (les filtres RC sont des filtres simples composés d'une résistance et d'un condensateur), etc.

Comme exemple d'application, prenons le mélangeur de tensions comme exercice. Le schéma ci-dessous le détaille: 

En appliquant ce théorème, nous obtenons U_AB telle que : \[ U_{AB} = \frac{\frac{E_{1}}{R_{1}} + \frac{E_{2}}{R_{2}}}{\frac{1}{R_{1}}+ \frac{1}{R_{2}}} \]

Et si R₁ = R et R₂ = 2R la tension U_AB sera égale à : \[ U_{AB} = \frac{\frac{E_{1}}{R} + \frac{E_{2}}{2R}}{\frac{1}{R}+ \frac{1}{2R}} = \frac{2 E_{1} + E_{2}}{3} = \frac{ {2}}{3}E_{1} + \frac{ {1}}{3}E_{2}\]

En conclusion, la tension U_AB sera composée des deux sources de tensions \( E_{1}\) et \( E_{2}\) telle que \( \frac{2}{3} E_{1}\) et \( \frac{1}{3} E_{2}\) soit une pondération à \( (\frac{2}{3},\frac{1}{3}) \)

Exercice d'application

Pour mieux comprendre cette théorie, nous vous proposons un exercice d'application avec une application directe en simulation éléctronique avec la solution LTSpice XVII : Application du théorème de Millman