L'inductance

D'après la théorie d'Ampère, tout fil parcouru par un courant électrique crée un champ électromagnétique dans le sens du mouvement du courant. L'inductance d'un circuit, le fil conducteur dans cas précis, se traduit donc par la valeur mesurée du flux magnétique créé par ce dernier (le flux magnétique représente la quantité de champ magnétique B qui traverse une surface S donnée).

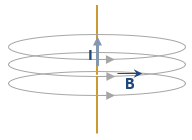
Il est aussi à l'origine de plusieurs autres solutions utilisées de nos jours, comme les bobines électriques, les transformateurs électriques, les générateurs par induction, etc.

Une inductance, également appelée solénoïde, bobine ou même parfois self. En se référant au principe décrit dans la théorie d'Ampère, une inductance en électronique et électrotechnique est un fil conducteur enroulé, dans la plupart des cas, autour d'un noyau en matériau ferromagnétique (une structure constituée d'éléments métalliques tels que le fer qui peut se transformer en aimant si la bobine est excitée électriquement) ou autour d'un assemblage de feuilles de tôle ou d'acier (en référence à la photo ci-dessous par Harrison Broadbent sur Unsplash : à gauche, une bobine enroulée sur un noyau ferromagnétique et à droite, juste à côté, un condensateur)

L'induction électromagnétique

L'induction électromagnétique, appelé aussi induction magnétique, est le phénomène inverse de l'induction comme décrit ci-dessous. En effet, si l'induction L est la résultante du passage du courant dans un fil conducteur et l'induction électromagnétique donne lieu à un courant induit suite à une force magnétique variable dans le temps.

C'est compliqué? Absolument pas, on vous simplifie les choses : les générateurs électriques, les turbines, le système de recherche par induction dans les téléphones mobiles de nos jours, etc., sont tous des bons exemples qui nous permettent de comprendre ce phénomène physique.

La génération de l'électricité par induction

Prenons comme exemple, un dynamo bouteille, appelé également dynamo sur roue (photo ci-dessous proposée par Ivan Radic sur Flickr), que nous utilisons dans nos bicyclettes, nous permet de transformer l'énergie mécanique en une énergie électrique à partir de la force mécanique.

La réponse d'une Self, comportement et réponse

Une self est réellement composée d'un fil conducteur enroulé sur un noyau ou sans. Sa principale caractéristique de ce dipôle est son comportement qui diffère en fonction de la nature du signal électrique qui le traverse. si ce courant est continu, la bobine se comporte comme un fil conducteur à faible résistance ohmique. Si la forme du courant électrique n'est pas continue, la forme du signal électrique aux bornes de la bobine sera différente.

Les deux courbes ci-dessous vous démontre le comportement d'une bobine losqu'elle est parcourue par un signal alternatif; la tension u(t) et l'intensité i(t) sont déphasées:

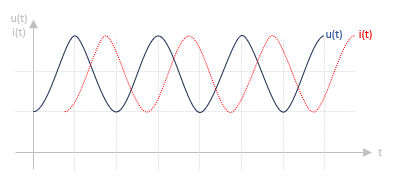
Pour écrire ce comportement mathématiquement, une bobine s'oppose à toute variation de courant électrique et se comporte comme une résistance en régime alternatif. Lorsque ce courant qui la traverse varie, il apparait une tension u à ses bornes suit cette formule:

\[ u = L\cdot \frac{di}{dt} \]

avec:

• u : la tension instantannée aux bornes de la bobine exprimée en Volt (V)
• L : la valeur inductive exprimée en Henry (H) de la bobine
• \( \frac{di}{dt} \) : représente la dérivée du courant i exprimé en Ampère (A)

Exemples d'applications d'une inductance

Ce composant est souvent utilisé pour filtrer les signaux électriques, dans les relais électriques, les moteurs, les transformateurs. Mais on le retrouve également dans les d'autres domaines d'applications comme:

• les circuit résonants : circuit composé de résistances, condensateurs et d'impédances (appelé généralement RLC)
• l'alimentation à découpage : la régulation est assurée par des éléments électroniques de puissance.
• les flashs électroniques (on les retrouvent dans les appareil photos ayant un système flash)
• etc.

Flux magnétique et inductance d'une bobine

L'inductance d'une bobine est mesurée en mH ou µH. L'unité de mesure de l'inductance est le Henry, nom donné à l'honneur du physicien Joseph Henry, dont le symbole est H.

Pour fabriquer une bobine électrique, on enroule n spirales d'un fil électrique de cuivre ayant un dimaètre Ø = d pour une longueur l sur un cylindre de diamètre extérieur Ø = D. La coupe ci-dessous détaille ces paramètres physique de la bobine :

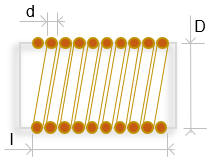
Pour déterminer la valeur de l'inductance L d'une bobine, il est nécessaire de mesurer du flux magnétique mesuré en Tesla (T), souvent noté Φ. Un fil conducteur parcouru par un courant I crée un champ magnétique (comme un aimant). Pour une surface donnée (celle de la bobine dans ce cas de figure), la valeur L, exprimée en Henry (H) s'écrit comme suit :

\[ L = n \cdot \frac{\phi}{I}  \enspace avec\enspace n:\enspace nombre \enspace de\enspace spirales\]

Or, l’intensité du flux magnétique Φ, exprimée en Weber (Wb), au centre d'une spire d'une bobine est donnée par l'équation suivante :

\[ \phi = π \cdot r^{2} \cdot \frac{µ_{0} I}{2πr} = π \cdot D \cdot I \cdot 10^{-7} \enspace (Wb) \]

\[ avec\enspace µ_{0} =4π \times 10^{-7}\enspace H\cdot m^{-1} \]

Ce qui résulte pour une bobine avec n spirales, la valeur de l'inductance L suivante :

\[ L = \frac{n}{I} \cdot π \cdot D \cdot I \cdot 10^{-7} = π \cdot \frac{l}{d}  \cdot D \cdot 10^{-7} H\]

Symbole d'une inductance (la bobine électrique)

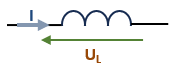
En électronique, une inductance est une bobine avec ou sans noyau ferromagnétique. Les deux figures ci-dessous représentent les deux schémas des deux types de bobines: 

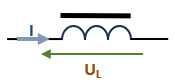Bobine sans noyau	Bobine avec noyau ferromagnétique

La valeur inductive de la bobine est calculée en général en fonction de son diamètre, de sa longueur et de la surface de son fil conducteur.

Mesure et code couleur

L'inductance d'une bobine quelle que soit sa forme et son type, est mesurée en Henrys (H). Avec plusieurs formes différentes, chaque forme une façon indique la valeur de son inductance différemment dont cette valeur est exprimée généralement en microHenry (µH). Particulièrement, nous retrouvons une forme d'inductance très similaire à la forme des résistances avec un code couleur dans le marché des composants électriques.

Comment lire le code couleur d'une inductances ?

Pour déterminer la valeur inductive d'une inductance, un code couleur peut être utilisé. Ce système de codage repose sur l'utilisation d'un tableau de référence pour les codes couleurs. Chaque couleur représentant un chiffre pour le 1^er digit, le 2^ème digit ou pour le facteur multiplicateur.

Dans certaines versions d'inductance, utilisées dans le domaine scientifique ou militaire, nous pouvons retrouver 5^ème bande, positionnée à l'extrémité gauche du composant, de couleur argent et dont la largeur est double.

Pour lire la valeur d'une inductance à bandes de couleur, nous pouvons faire référence à ce tableau ci-dessous :

Attention : comme pour les résistance, vous devez adopter les bonnes pratiques pour une lecture correcte. Les deux remarques ci-dessous reste valables:

• Vous devez placer l'anneau de tolérance à droite pour ne pas lire à l'envers.
• L'anneau de tolérance est plus écarté par rapport les autres anneaux.

Et à ne pas oublier, la phrase fameuse mnémotechnique pour vous vous rappeler de l'odre exact des codes couleurs: Ne Manger Rien Ou Jeûner Voilà Bien Votre Grande Bêtise.

Nous avons mis en place un calculateur de code couleur des inductances à 3 et 4 bandes qui vous permet de calculer la valeur inductive en µH des inductances à partir des différentes couleurs d'anneaux imprimés sur le corps de ce dipôle.

Inductances en parallèle et en série

Pour calculer la valeur équivalente en H (Henry) de plusieurs inductances en parallèle ou en série, les règles ci-dessous sont à appliquer :

• en série : la valeur équivalente en Henry d'un ensemble d'inductances en série est égale à la somme des différentes valeurs L de chaque inductance dans le circuit.

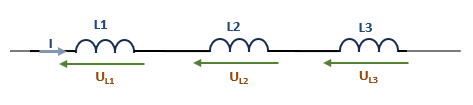Et sous forme mathématique, nous écrivons cela comme suit :\( L_{éq} = \sum{L_{i}} \)

Ce qui donne d'après le schéma ci-dessus l'équation suivante : \( L_{iéq} = L_{1} + L_{2} + L_{3} \)

• en parallèle : la valeur équivalente inversée en Henry est calculée à partir de la somme des inverses de toutes les inductances H_i dans notre circuit.

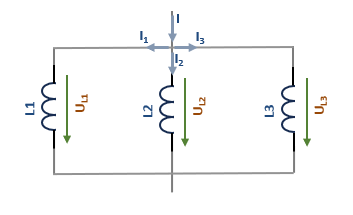Donc, sous forme mathématique, nous écrivons cela comme suit :\( \frac{1}{L_{éq}} = \sum{\frac{1}{L_{i}}} \)