Les condensateurs
Un condensateur, ou capacitor en anglais, est un composant électronique constitué de deux plaques conductrices séparées par un matériau isolant, appelé diélectrique (photos ci-dessous de transistors céramiques par shed sur Freeimages).

Il est utilisé dans divers circuits pour gérer l’énergie, notamment dans les filtres, les circuits de découplage et les alimentations électriques. Avec l’évolution technologique, la conception des condensateurs s’est diversifiée, et ils se présentent aujourd’hui sous des formes variées telles que cylindriques, planes ou autres, selon les besoins spécifiques des applications. Les matériaux diélectriques ont également évolué, passant du papier ou du verre à des plastiques comme le polyester ou le polypropylène, offrant ainsi des condensateurs plus compacts, plus efficaces et plus adaptés aux exigences des circuits modernes. Ces composants sont essentiels dans de nombreux dispositifs électroniques, permettant une gestion optimale de l’énergie et des signaux.
A quoi sert un condensateur ?
Le condensateur a la capacité d'emmagasiner une charge électrique durant la phase de charge, puis de la libérer à la demande (on appelle cette phase la phase de déchargement). Ce composant peut également servir à temporiser, à retarder, ... en fonction de son utilité dans le circuit électrique. La capacité d'un condensateur est exprimée en F (Farad) et les l'ordres de grandeur de la capacité de ce composant est généralement à l'ordre de pF (picofarads) ou µF (microfarads).
Un condensateur est constitué de deux électrodes métalliques séparées électriquement par un matériau non conducteur appelé de diélectrique :
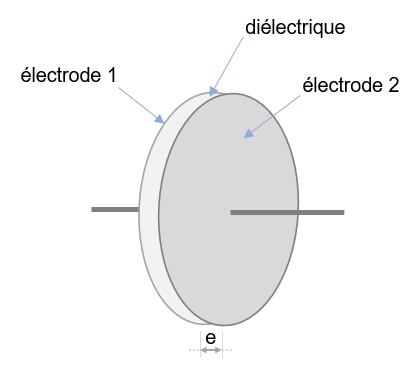
Les unités de la capacité électrique
L'unité de base dans le système international d'unités est le Farad dont le symbole est le F. En réalité, cette unité est extrêmement vaste. Ses sous-multiples, microfarad (symbole : μF), nanofarad (symbole : nF) et picofarad (symbole : pF), sont généralement utilisés. Les unités dérivées qui permettent d'exprimer des capacités à différentes valeurs sont donc comme suit:
| Unité | Symbole | Equivalence | Description |
| PicoFarad | pF | 1 nF = 10⁻12 F | un décifarad de Farad, couramment utilisé dans les composants électroniques |
| NanoFarad | nF | 1 nF = 10⁻9 F | un milliardième de Farad, utilisé fréquemment dans les circuits électroniques. |
| MicroFarad | µF | 1 μF = 10⁻6 F | un millionième de Farad, Il s'agit d'une unité fréquemment employée pour les condensateurs dans les appareils électroménagers et dans les applications électroniques générales. |
| MilliFarad | mF | 1 mF = 10⁻3 F | représente un millième de Farad, rarement utilisé en électronique, utilisé pour les condensateurs de plus grande capacité, souvent dans des systèmes de puissance |
| Farad | F | 1 F | unité de base de la capacité électrique dans le Système International (SI) |
Ces différentes sous-unités permettent d'adapter la mesure de la capacité à une large gamme de composants et de circuits électriques, allant des plus petits condensateurs jusqu'aux systèmes d'emmagasinage de l'énergie électrique.
Comment calculer sa charge q ?
La charge q stockée et la tension U aux bornes du condensateur sont liées par la relation suivante :
\[ q = C \times U \]
avec :
- U : la tension aux bornes du condensateur mesurée en Volts (V)
- C : la capacité du condensateur mesurée en Farads (F)
- q : la charge positive exprimée en Coulombs (C)
Comment calculer l'énergie emmagasinée ?
Un condensateur idéal nous permet de stocker de l'énergie électrique durant la phase d'excitation ( ce qu'on appelle la phase de charge comme expliqué au début de cette section) et de nous la fournir lorsqu'elle est demandée par notre circuit électrique. Cette fonction de stockage de l'électricité n'est réellement valable que dans le régime du courant continu (en DC). En effet, en régime du courant alternatif (en AC), un condensateur s'opposant aux variations de la tension de potentielle et bloque le transfert de cette énergie emmagasinée.
Pour fonctionner, un condensateur dépense de l'énergie pour se charger, puis la restitue lorsqu'il se décharge. Cette énergie dissipée W conduit à un courant variable qui possède toutes les propriétés du courant électrique est qui est proportionnelle au produit de la charge q emmagasinée par la tension de charge U.
Ainsi, pour calculer l'énergie emmagasinée dans le champ électrique entre ses plaques, nous admettons la formule suivante :
\[W = \frac{1}{2}q\,U \]
avec :
- U : la tension aux bornes du condensateur mesurée en Volts (V)
- q : la charge positive exprimée en Coulombs (C)
- W : l'énergie emmagasinée par le condensateur exprimée en Joule (J)
En utilisant la formule q = C x U, on peut aboutir aux 2 autres formules équivalentes pour déterminer la valeur de l'énergie emmagasinée :
\[ W = \frac{1}{2}C\, U^{2} \enspace ou \enspace W=\frac{1}{2}\frac{q^{2}}{C} \]
Quelle relation entre le courant et la tension ?
La relation entre l'intensité i du courant électrique qui traverse un condensateur idéal, la différence de potentiel entre ces deux bornes et la capacité du condensateur, le courant i est égal à :
\[ i = C \; \frac{du}{dt} \]
avec :
- \( \frac{du}{dt} \) : dérivé de la différence de potentiel aux bornes du condensateur. Si la tension u est constante dans le temps, le courant i qui traverse le condensateur sera nul.
- C : la capacité du condensateur expirmée en Farad (F)
Symbole et différents types
Pour modéliser un condensateur, deux lignes parallèles représentent les deux électrodes du composant, séparées par un petit espace représentant le diélectrique. L'image ci-dessous représente cette schématisation électrique :
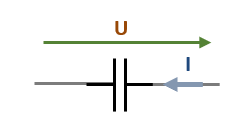 Ce composant joue un rôle fondamental dans l’électronique d’aujourd’hui. En effet, il est présent dans la plupart des assemblages et montages électriques et/ou électroniques sous plusieurs formes. C'est pourquoi il est capital de bien comprendre son fonctionnement.
Ce composant joue un rôle fondamental dans l’électronique d’aujourd’hui. En effet, il est présent dans la plupart des assemblages et montages électriques et/ou électroniques sous plusieurs formes. C'est pourquoi il est capital de bien comprendre son fonctionnement.
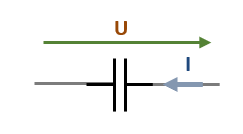
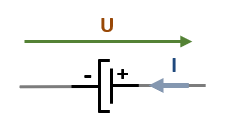
Les différentes variantes sont principalement quatre :
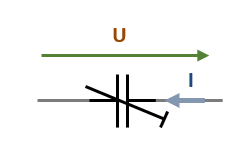
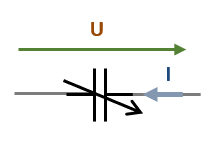
| Non-polarisé | Polarisé | Ajustable | Variable |
 |
 |
 |
 |
Différents types de condensateurs
Sur le marché de nos jours, il existe plusieurs formats et types de condensateurs en fonction de l'usage final dont les plus importants sont énumérés ci-dessous :
- Condensateur céramique: c'est un composant électrique à diélectrique céramique (souvent du dioxyde de titane, TiO₂, un composé chimique formé d'atomes de titane et d'oxygène). Compact et robuste, il est utilisé dans les circuits de découplage, de filtrage et de stabilisation à faible coût et avec une haute fiabilité.
- Condensateur à film: il s'agit de condensateurs dont le diélectrique est un film plastique (polyester, polypropylène, etc.) offrant une faible perte et une grande stabilité. Ils sont utilisés dans les applications nécessitant précision et fiabilité (audio, alimentation).
- Condensateur électrolytiques: ce dipôle à électrolyte comme électrode, polarisé et offrant une capacité élevée, est utilisé dans les circuits de filtrage et de découplage de puissance à faible coût.
- Supercondensateur: cette version de condensateur à double couche électrochimique (EDLC) offre une densité énergétique élevée à faible tension. Ils sont utilisés pour le stockage rapide d’énergie dans des véhicules électriques, des dispositifs à haute fréquence de charge/décharge, etc.
- Condensateur mica: ce sont des condensateurs à faible perte et haute précision, utilisant du mica comme diélectrique, utilisés dans les applications haute fréquence et de télécommunication où la stabilité est critique.
- Condensateur en verre: constitué du verre comme diélectrique, résistant aux conditions extrêmes (température, humidité), utilisé dans des applications industrielles ou aérospatiales nécessitant une robustesse maximale.
- Condensateur de traversée: ce type de condensateur à montage traversant pour les circuits imprimés permet une connexion via des trous traversants et optimise l'espace sur la surface du PCB.
- Condensateur ajustable: la capacité en Farad est réglable manuellement. Il est utilisé pour l'ajustement fin des circuits, comme dans les circuits d’accord (radios, appareils de précision).
Identification et code couleur
Pour identifier la valeur d'un condensateur, il est nécessaire d'en connaître le type au préalable. D'ailleurs, certains condensateurs sont identifiables par une écriture directe (un simple affichage en clair), d'autres par un codage particulier et d'autres encore par un code couleurs.
Pour le marquage en clair, il n'y a aucune difficulté à lire la valeur capacitive sur le condensateur. Dès que le symbole F ou le mot Farad n'est pas indiquée, et que la sous-unité n'est pas mentionnée non plus, une compréhension est nécessaire pour lire la valeur inscrite. Ci-dessous quelques exemples :
| Valeur indiquée sur le condensateur | valeur correspondante (F) |
| 20 | 20µF |
| 3n3 | 3.3nF |
| .001 | 0.001µF = 1nF |
Pour un marquage chiffré, la valeur capacitive du condensateur est généralement exprimée en trois chiffres. Les deux premiers indiquent la valeur significative et le troisième est le facteur multiplicatif. Certaines indications sont suivies d'une lettre pour compléter une information complémentaire sur la tolérance.
Pour les condensateurs céramiques, un codage spécial a été adopté. Le tableau ci-dessous résume ce qui précède :
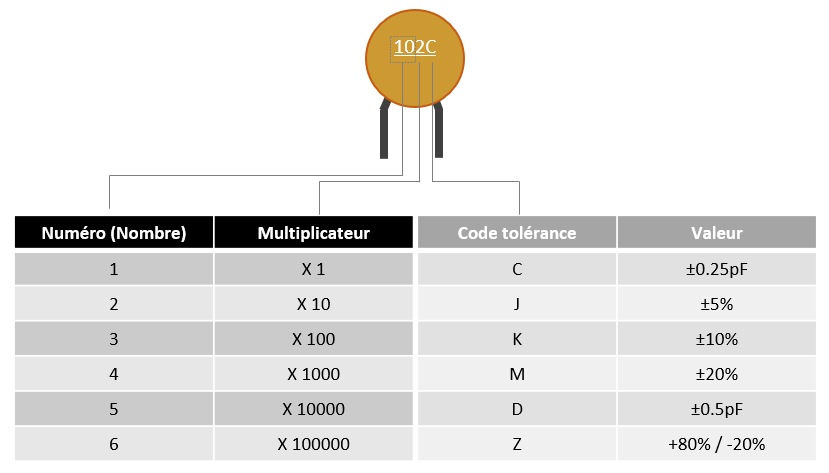
En fonction de son milieu d'utilisation et de son application dans l'industrie, un condensateur céramique doit être bien choisi. En effet, sa température de fonctionnement a un rôle primordial sur son rendement. Pour une meilleure classification, les deux normes EIA-198 et puis évolué à EIA RS-198 ont été mises en place pour identifier et déterminer la valeur à indiquer sur chaque condensateur si nécessaire. Cette indication, composée de 3 lettres comme Y5F, Y5U, Z5V, etc., détaille les caractéristiques de fonctionnement en fonction de la température.
Le tableau ci-dessous résume la correspondance pour la norme EIA RS-198 :
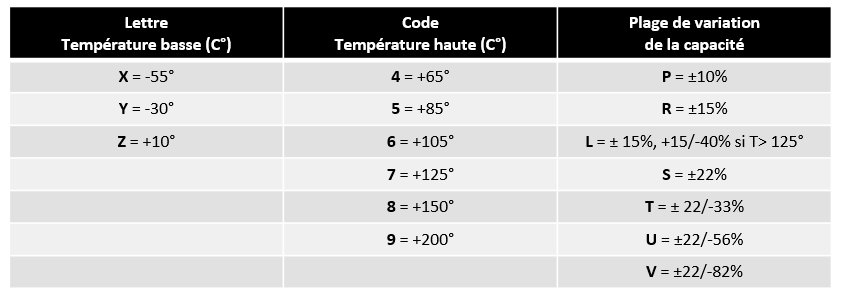
Il est à noter que d'autres tableaux de correspondance existent. Il est fortement recommandé de consulter la fiche technique fournie par le constructeur lors du choix de vos composants.
Pour le codage à couleur, en général, peu importe le type de condensateur et le constructeur, la relation entre les couleurs et les valeurs numériques est quasiment identique, et elle est détaillée dans le tableau ci-dessous :
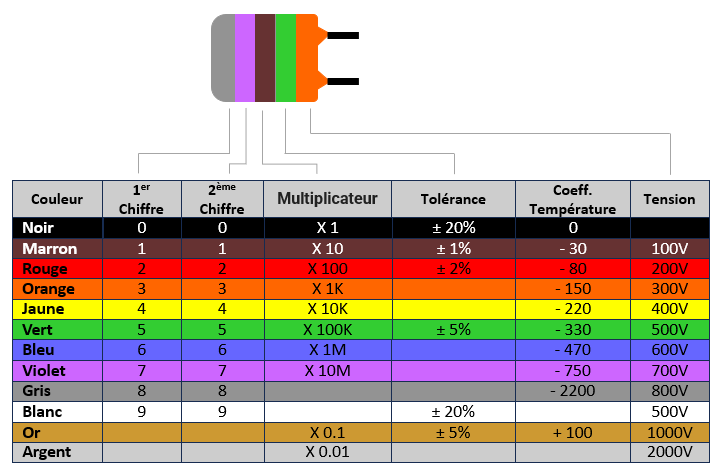
Et pour bien mémoriser l’ordre de ces codes, nous pouvons appliquer la même phrase mnémotechnique celle utilisé pour les résistances : « Ne Manger Rien Ou Jeûner Voilà Bien Votre Grande Bêtise »
Condensateur en parallèle et en série
Pour calculer la valeur exacte en Farad de plusieurs condensateur en parallèle ou en série, les règles ci-dessous doivent être appliquées :
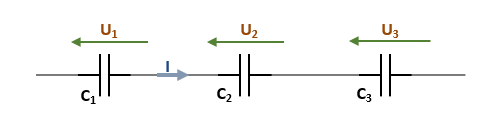
- En série, la valeur capacitive en F équivalente d'un ensemble de condensateurs en série est égale à la somme des inverses de toutes les capacités en object.
 Et sous forme d'équation, nous écrivons cela comme ci-dessous :
Et sous forme d'équation, nous écrivons cela comme ci-dessous :
\[ C_{éq} = \sum{\frac{1}{C_{i}}} \]
Ce qui donne pour notre cas de figure ci-dessus l'équation suivante :
\[ C_{éq} = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}} \enspace ce\enspace qui\enspace donne\enspace C_{éq} = \frac{C_{1}\times C_{2}\times C_{3}}{C_{1}+C_{2}+C_{3}} \]
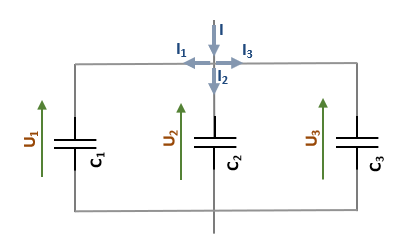
- En parallèle : la valeur capacitive équivalente en F est calculée à partir de la somme des inverses de toutes les résistances en question.
Et sous forme d'équation, nous écrivons cela comme ci-dessous :
\[ C_{éq} = \sum{C_{i}} \]
Ce qui donne d'après le schéma ci-dessus l'équation suivante : \[ C_{éq} = C_{1} + C_{2} + C_{3} \]
| < Les résistances | Les composants | Les diodes > |