La résistance électrique
La résistance électronique, également appelée résistor, conducteur ohmique ou résistance électrique, est un composant indispensable dans les circuits électroniques. Elle joue un rôle crucial en limitant le passage du courant électrique, protégeant ainsi les autres composants du circuit contre les risques de surintensité. En régulant le flux de courant, la résistance électronique permet également de contrôler la tension entre les bornes d'un composant, ce qui est essentiel pour assurer le bon fonctionnement de l'ensemble du système.
La valeur de la résistance électrique est déterminée par la relation entre l'intensité du courant qui la traverse et la tension appliquée à ses bornes. Cette relation est régie par la fameuse loi d’Ohm, formulée par le physicien allemand Georg Simon Ohm en 1827. La loi d'Ohm établit que la tension (U) est proportionnelle à la résistance (R) et à l'intensité du courant (I) qui traverse la résistance. L'équation correspondante est la suivante:
\[ U = R \times I \]
avec :
- U: la tension mesurée en Volts V
- R : la résistance mesurée en Ohms Ω
- I : l’intensité du courant mesurée en Ampers A
Les différents types de résistances électriques
Dans le domaine de l'électronique, on trouve plusieurs types de résistances électriques (formes, topologies, modèles), chacun ayant des caractéristiques adaptées à des besoins spécifiques tels que :
- Les résistances à couche de carbone: les résistances à couche de carbone (photo ci-dessous par Keyvan Max sur Unsplash) sont fabriquées en déposant une fine couche de carbone sur un substrat en céramique. Elles sont largement utilisées dans des applications où la précision n'est pas critique, mais où la résistance électrique doit être abordable. Elles sont souvent identifiées par un code couleur de résistance qui permet de déterminer la valeur de la résistance en fonction des couleurs des anneaux imprimés sur leur corps.

- Les résistances à couche métallique: Contrairement aux résistances à couche de carbone, les résistances à couche métallique sont fabriquées avec un métal conducteur. Elles sont souvent utilisées dans des circuits où la précision est importante, car elles ont une tolérance plus faible et sont plus stables thermiquement.
- Les résistances bobinées: Ces résistances sont composées d'un fil métallique enroulé autour d'un noyau isolant. Elles sont adaptées pour dissiper de fortes puissances et sont couramment utilisées dans des applications où des courants importants doivent être contrôlés sans surchauffer.
- Les résistances CMS (Composants Montés en Surface): Les résistances CMS sont des composants compacts qui se soudent directement à la surface des cartes de circuits imprimés (PCB). Ces résistances sont particulièrement populaires dans la fabrication de dispositifs électroniques miniaturisés, comme les téléphones mobiles et les ordinateurs portables.
- Les résistances en réseaux: Ces résistances regroupent plusieurs valeurs de résistance dans un seul boîtier. Elles sont souvent utilisées dans des circuits où plusieurs résistances doivent être connectées en parallèle ou en série pour obtenir la résistance totale souhaitée.
- Les résistances en boîtier SIP (Single Inline Package): Ces résistances sont utilisées dans des configurations de circuits où l'espace est limité. Elles sont souvent montées sur une seule rangée de broches, ce qui permet un montage rapide et efficace.
Résistivité, Conductivité et Conductance
La résistance d'un dipôle dépend à la fois de la nature du composant et de ses dimensions. La résistance R d'un fil conducteur, exprimé en Ohm(Ω), est proportionnelle à sa longueur, mais inversement proportionnelle à sa section, telle que: \( R = \rho \frac{L}{S} \)
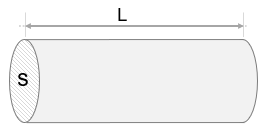
La résistivité d'un dipôle dépend de celle de la nature des matériaux qui le constituent. En effet, la résistivité est une caractéristique électrique de chaque matérière. Elle est représentée par ρ (rhô en lettre grec) et son unité est l'ohm-mètre (Ω·m). Ce coefficient, exprimé en Ohm-mètre (Ωm), est déterminé dans des conditions prédéfinies. Le tableau ci-dessous représente les résistivités des principaux métaux purs et des alliages couramment utilisés en génie électrique :
| Matière | La résistivité ρ (déterminé à 20° C) |
| Argent (Ag) | 1.68 x 10-8 8 Ω⋅m |
| Cuivre (Cu) | 1.7 x 10-8 8 Ω⋅m |
| Aluminium (Al) | 2.82×10−8 Ω⋅m |
| Tungstène (W) | 5.6×10−7 Ω⋅m |
| Fer (Fe) | 1.00×10−7 Ω⋅m |
| Argent (Ag) | 1.59×10−8 Ω⋅m |
| Acier inoxydable | 7.2×10−7 Ω⋅m |
| Platine (Pt) | 1.06×10−7 Ω⋅m |
| Plomb (Pb) | 2.2×10−7 Ω⋅m |
| Or (Au) | 2.44×10−8 Ω⋅m |
| Nickel (Ni) | 6.99×10−8 Ω⋅m |
| Mercure (Hg) | 9.58×10−7 Ω⋅m |
| Carbone (graphite) | 3×10−5 Ω⋅m |
La conductivité d'un matériau, exprimée en Siemens par mètre (S/m), est mathématiquement l'inverse de la résistivité, telle que :
\[ \sigma =\frac{1}{\rho} \]
On appelle aussi la conductance d'un dipôle G, exprimé en Siemes (S), par simplement l'inverse de la résistivité R, telle que:
\[ G =\frac{1}{R} \]
Symbole, mesure et code couleur
Le symbole suivant représente une résistance :
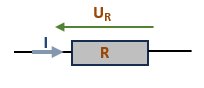
La représentation mathématique de cette relation \( U(t) = R \cdot I(t) \) est définie par une doite qui passe par l'origine (0,0) dont le coefficient est la valeur ohmique R de notre dipole.

Cette valeur ohmique est généralement identifiée par un code de couleurs représenté par des anneaux. Cette représentation est universelle et normalisée.
Comment lire le code couleur des résistances?
Pour déterminer la valeur ohmique d'une résistance électrique, un code de résistance est utilisé. Ce système repose sur l'utilisation de couleurs de résistance, chaque couleur représentant un chiffre ou un facteur multiplicateur, le tableau de codage ci-dessous détaille les différents code couleur des résistances que nous pouvons retrouver sur une résistance:
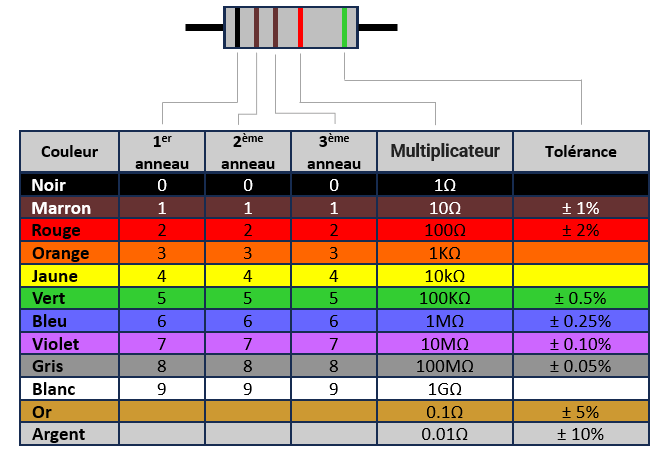
Ce code couleur de résistance est essentiel pour déchiffrer rapidement les spécifications des résistances, sans avoir besoin de calculs complexes. Il est généralement composé de quatre anneaux colorés ou de cinq anneaux imprimés sur le corps de la résistance. Le premier, le deuxième (dans le cas d'une résistance à quatre anneaux) et parfois le troisième anneau (dans le cas d'une résistance à cinq anneaux) représentent les chiffres significatifs, tandis que le quatrième (ou le cinquième en fonction du nombre de cercles imprimés sur la résistance) anneau représente le multiplicateur ou la tolérance à appliquer.
Attention : pour une lecture correcte, il est important de noter les deux remarques suivantes:
- Vous devez placer l'anneau de tolérance à droite pour ne pas lire à l'envers.
- L'anneau de tolérance est plus écarté par rapport les autres anneaux.
Et pour bien mémoriser l’ordre de ces codes, voilà une phrase mnémotechnique : Ne Manger Rien Ou Jeûner Voilà Bien Votre Grande Bêtise.
Les unités de résistance électrique
L'unité de base dans le système international d'unités est l'ohm dont le symbole est : Ω. Outre l'unité de base, il existe des unités dérivées pour exprimer des résistances à des valeurs variées telle que:
| Unité | Symbole | Equivalence | Description |
| NanoOhm | nΩ | 1 nΩ = 10⁻⁹ Ω | un milliardième d'ohm, utilisé dans des contextes de mesure de résistances ultra-faibles, comme dans les nano-technologies. |
| MicroOhm | µΩ | 1 μΩ = 10⁻⁶ Ω | un millionième d'ohm, utilisé pour des résistances extrêmement faibles, souvent dans des matériaux très conducteurs. |
| MilliOhm | mΩ | 1 mΩ = 10⁻³ Ω | représente un millième d'ohm, utilisé pour mesurer des résistances très faibles, comme dans les fils conducteurs. |
| Ohm | Ω | 1 Ω | unité de base de la résistance dans le Système International (SI) |
| KiloOhm | KΩ | 1 kΩ = 10³ Ω | représente mille ohms, utilisé pour des résistances communes dans les circuits électroniques. |
| MégaOhm | MΩ | 1 MΩ = 10⁶ Ω | un million d'ohms, utilisé pour des résistances élevées, souvent dans des composants comme les résistances de protection. |
| GigaOhm | GΩ | 1 GΩ = 10⁹ Ω | un milliard d'ohms, utilisé pour des résistances très élevées, par exemple dans des isolants ou des matériaux utilisés dans les circuits haute tension. |
Ces différentes sous-unités permettent d'adapter la mesure de la résistance à une large gamme de composants et de circuits électriques, allant des faibles résistances dans les conducteurs fins jusqu'aux résistances très élevées dans les isolants ou les composants électroniques spécifiques.
Comment mesurer la valeur d'une résistance ?
En cas d'indisponibilité de la valeur de la résistance R indiquée sur le composant, d'absence d'anneaux de code couleurs ou de l'effacement de certains d'entre eux, il est possible de la mesurer directement avec un ohmmètre (instrument permettant de mesurer la valeur de la résistance d'un composant électrique) ou de la calculer en effectuant une mesure des deux composantes U et I. En appliquant directement la formule de la loi d'Ohm, nous pouvons déterminer sa ohmique en Ω.
Pour cela, il est nécessaire de disposer de deux équipements de mesure : un ampèremètre et un voltmètre. Le montage ci-dessous décrit la méthode à suivre :
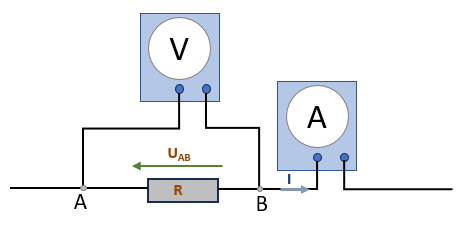
Pour mesurer la tension UAB entre les points A et B, le voltmètre doit être branché en parallèle avec la résistance. Et pour mesurer le courant I qui traverse la résistance, il faut utiliser un ampèremètre branché en série avec celle-ci. Ainsi la valeur de la résistance R sera égale à : \( R = \frac{U_{AB}}{I} \)
L'effet Joule
Une résistance parcourue par un courant électrique consomme, comme tout composant, de l'énergie. Dans le cas d'une résistance, cette énergie est dissipée sous forme de chaleur, s'exprime \( P_{d} = UI \) et grace grace à la loi d'Ohm, elle peut prendre ces 3 formes :
\[ P_{d} = U I= RI^{2}=\frac{U^{2}}{R} \]
Résistances en parallèle et en série
Pour calculer la valeur exacte ohmique en ohm (Ω) de plusieurs dipôles résistifs montés en parallèle ou en série, nous pouvons appliquer les les règles ci-dessous s'appliquent :
Résistances en série
La valeur équivalente en ohm d'un groupement de résistances en série est égale à la somme des valeurs respectives de chaque dipôle telle que:
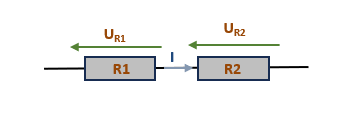 Soit en formule mathématique, nous l'écrivons comme ci-dessous: \( R_{éq} = \sum{R_{i}} \)
Soit en formule mathématique, nous l'écrivons comme ci-dessous: \( R_{éq} = \sum{R_{i}} \)
Ce qui donne, d'après le schéma ci-dessus, l'équation suivante la formule suivante : \( R_{éq} = R_{1} + R_{2} \)
Démonstration pour des résistancess en série:
Soit le schéma ci-dessous d'un regroupe de n résistances montées en série:
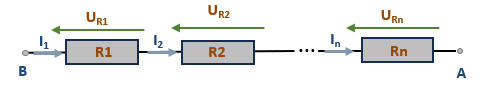
Et en appliquant la formule de la loi d’Ohm, nous pouvons écrire l'équation suivante pour écrire la tension UAB en les deux points A et B:
\( U_{AB} = R_{1} \cdot I_{1} + R_{2} \cdot I_{2} + \enspace ... \enspace + R_{n} \cdot I_{n} \) avec \( I = I_{1} = I_{2} = \enspace ... \enspace = I_{n} \)
Ce qui fait donc \( R_{éq} = \frac{U_{AB}}{I} = R_{1} + R_{2} + \enspace ... \enspace + R_{n} \) d'où \( R_{éq} = \frac{U_{AB}}{I} = \sum {R_{i}} \)
Résistances en parallèles
La valeur équivalente inversée en Ohm est calculée à partir de la somme des inverses de toutes les résistances en question.
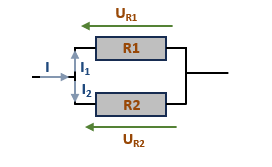
Et sous forme d'équation, nous écrivons cela comme ci-dessous : \( \frac{1}{R_{éq}} = \sum{\frac{1}{R_{i}}} \)
Ce qui donne d'après le schéma ci-dessus l'équation suivante : \( \frac{1}{R_{éq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} \)
Démonstration pour des résistancess en parallèle:
Soit le schéma ci-dessous d'un regroupe de n résistances montées en parallèle:
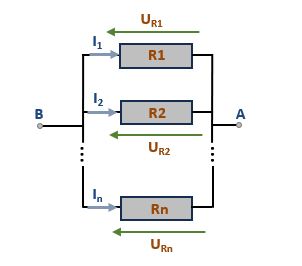
En appliquant la formule de la loi d’Ohm et la loi des nœuds, nous écrivons les deux équations suivantes pour la tension UAB en les deux points A et B:
- \( U_{AB} = U_{R1} = U_{R2} = \enspace ... \enspace = U_{Rn} \)
- \( I = I_{1} + I_{2} + \enspace ... \enspace + I_{n} \) d'après la loi des noeuds au point A (une des lois de Kirchhoff)
Ce qui donne : \( \frac{U_{AB}}{R_{eq}} = \frac{U_{R1}}{R_{1}} + \frac{U_{R2}}{R_{2}} + \enspace ... \enspace + \frac{U_{Rn}}{R_{n}} \) soit \( \frac{1}{R_{eq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \enspace ... \enspace + \frac{1}{R_{n}} = \sum{\frac{1}{R_{i}}} \)
Résistances en montage mixte
Dans le cas de plusieurs résistances montées en série et en parallèle, il est demandé de déterminer la résistance équivalente du circuit afin de simplifier la compréhension et l'analyse du montage électrique. Cette notion de la résistance équivalente est cruciale lorsqu'il s'agit de circuits combinant des résistances en série et en parallèle. Pour cela, il est recommandé de chercher les deux valeurs \( R_{eq1} \) et \( R_{eq2} \), qui permettent de réduire le montage complexe à deux dipôles. Une fois ces deux valeurs calculées, il est possible de les monter en parallèle ou en série, ce qui facilite le calcul de la valeur ohmique équivalente globale du circuit.
Dans les circuits combinant des résistances en série et en parallèle, il est habituel de procéder par étapes. La première consiste à calculer les résistances équivalentes pour chaque sous-ensemble du circuit. Ensuite, ces résistances équivalentes sont regroupées, soit en série, soit en parallèle, jusqu'à ce qu'une seule résistance équivalente soit obtenue pour l'ensemble du montage. Ce processus de simplification est particulièrement précieux pour les ingénieurs et concepteurs de circuits, car il permet de réduire la complexité du circuit tout en facilitant le calcul de la valeur ohmique équivalente totale. Cette valeur pourra ensuite être utilisée pour d'autres analyses ou ajustements du circuit.
Cas de résistances de même valeurs
Un cas très particulier est assez souvent utilisé en électronique est celui de doublement de résistances de même valeur R tel que :
- en série: la valeur de la résistance équivalente sera le double de la valeur unitaire ( \( R_{eq}=2R \) )
- en parallèle: la valeur de la résistance équivalente sera la moitié de la valeur unitaire ( \( R_{eq}=\frac{R}{2} \) )
L'effet de Joule et la dissipation thermique
Lorsqu'un courant électrique traverse une résistance génère une énergie calorifique qui est dissipée de manière indirecte. Cette énergie peut parfois s'avérer bénéfique dans notre vie quotidienne, exemple le chauffage électrique, la plaque de cuisson, etc. mais elle peut aussi s'avérer totalement inefficace, comme dans le cas de la télévision.
Cette énergie dissipée par effet de Joule pour un courant continu mesurée en Joules (J) est égale à : \[ Q = R \times I^2 \times t \]
Et la puissance dissipée par effet Joule en courant continu mesurée en Watts (W) est égale à : \[ P = R \times I^2 \]
avec :
- R : la résistance mesurée en Ohms Ω
- I : l’intensité du courant mesurée en Ampers A
- t : la durée du temps exprimée en Secondes s
| < L'alimentation électrique | Les composants | Les condensateurs > |