Le système hexadécimal
Structure d'un nombre hexadécimal
Un nombre hexadécimal peut être décomposé et écrit sous la forme d'une suite de puissances de 16 (comme pour le système octal, dont chaque chiffre est placé dans une position correspondant à une puissance de 8), chaque chiffre de ce système représentant un rang spécifique, tout en ayant la valeur la plus petite \( 8^{0} = 1 \) pour la valeur 1.
Par exemple, le nombre hexadécimal 0x4E peut être décomposé ainsi comme suit : \( 4 \times 16^{1} + E \times 16^{0} \). Le préfixe 0x, qui précède le nombre 4E, n'est qu'une indication en informatique qui signifie que la suite représente un nombre hexadécimal.
Ce qui nous donne, si nous souhaitons convertir ce nombre hexadécimal 0x4E en valeur décimale, le résultat 78 en base 10. En effet, le système hexadécimal sert à convertir les nombres binaires complexes en une forme plus simple mathématiquement et lisible tout en permettant de simplifier la manipulation des entiers ou des nombres flottants dans les systèmes de calculs logiques tels que les microcontrôleurs, les processeurs, etc.
Exemple de décomposition et conversion : le décodage
Pour décoder un nombre hexadécimal, comme expliqué précédemment dans le chapitre consacré au codage, au décodage et au transcodage, il est demandé de réécrire le nombre dans une suite de puissances de 16. Si le nombre équivalent en décimal est recherché, la somme de chaque produit donnera la résultante en base dix. Par exemple, le nombre hexadécimal 0x1A3F ou tout court 1A3F sera ainsi écrit:
- 1 représente \( 1 \times 16^{3} = 1 \times 4096 = 4096 \),
- A représente \( A \times 16^{2} = 10 \times 256 = 2560 \),
- 3 représente \( 3 \times 16^{1} = 3 \times 16 = 48 \),
- F représente \( 15 \times 16^{0} = 15 \times 1 = 15 \).
En additionnant toutes ces valeurs, nous obtenons l'équivalent du nombre 0x1A3F en décimal tel que:
\[ 1 \times 16^{3} + 10 \times 16^{2} + 3 \times 16^{1} + 15 \times 16^{0} = 1 \times 4096 + 10 \times 256 + 3 \times 16 + 15 \times 1 = \]Ainsi, 1A3F en hexadécimal (en base 16) correspond à 6719 en décimal (en base 10)
Les opérations arithmétiques en hexadécimal
Les opérations arithmétiques comme l'addition, la soustraction, la multiplication et la division peuvent être effectuées sur des nombres hexadécimaux de la même manière que dans le système décimal. Cependant, en numération hexadécimale, Il est important de prendre en compte les règles de retenue spécifiques à ce système en base de 16. Les divisions euclidiennes sont souvent utilisées pour effectuer des conversions entre les différents systèmes numériques.
Pourquoi utiliser le système hexadécimal ?
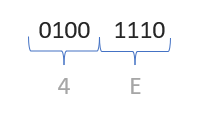
Le système de numérotation hexadécimal est une représentation binaire compressée qui permet de travailler avec de grands nombres binaires. Cela permet de représenter un octet informatique (un octet informatique est une représentation de 8 signaux électriques) avec seulement deux caractères hexadécimaux et rend la gestion des données beaucoup plus facile et rapide. En effet, chaque nombre hexadécimal est codé sur 4 bits, ce qui facilite la lecture de toutes les informations numériques, chaque caractère ou octet se réduisant à 2 chiffres dans le système hexadécimal. Le mot binaire 0100 1110 soit l'équivalent en système hexadécimal du mot 0x4E s'écrit ainsi comme suit:
Pour mieux comprendre l'utilité de ce sytème, vous trouverez ci-dessous quelques exemples d'application de ce codage dans le système hexadécimal:
- La représentation des caractères alphanumériques; par exemple la table de codage ASCII, pour l'abréviation en anglais de : American Standard Code for Information Interchange.
- l'adressage mémoire, table d'indexation sur les disques de stockage, ... exemple. : 0x8FAF.
- la représentation des codes couleurs dans la modélisation web en langue HTML, CSS ou autre. Par exemple, le #008000 représente la couleur verte et le #FF0000 représente la couleur rouge, etc.
- le codage des données dans les calculateurs, les unités logiques, les processeurs, ... est implémenté en format hexadécimal pour faciliter la lecture des nombres représentés électriquement en format binaire et pour permettre aux développeurs, ingénieurs et amateurs de mettre en place des codes et des programmes plus facilement.