Le système décimal
Le système décimal, appelé aussi le système à base 10, est un système de numérotation qui utilise la série de chiffres allant de 0 à 9. C'est le système le plus fréquemment utilisé dans notre vie quotidienne, en particulier pour effectuer des calculs, mesurer et noter les nombres. Chaque position d'un chiffre dans un nombre décimal possède une pondération en fonction de sa position. C'est ce qu'on appelle couramment le chiffre des dizaines, des centaines, des milliers, ... En effet, cette position représente une valeur égale à une puissance de 10, ce qui permet de représenter des valeurs allant de la très petite à la plus grande valeur possible si nous combinons les chiffres avec les multiples de 10.
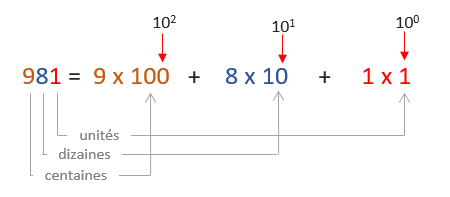
Par exemple, le numéro 981 est une suite de trois chiffres telle que (la figure ci-dessous explique ce calcul):
- le chiffre 9 représente les centaines dans ce nombre, soit \(10^{2} = 100\).
- Le chiffre 8 représente le nombre des dizaines, soit \(10^{1} = 10\).
- Le chiffre 1 se trouve dans la position des unités.
Ainsi, chaque chiffre de ce nombre possède une pondération en fonction de sa position. Ce qui donne un poids différent pour chaque chiffre dans notre nombre y compris le chiffre 0. Par contre, ajouter un ou plusieurs zéros à gauche dans un nombre n'affecte pas sa valeur. Par exemple, l'écriture 00981 est égal à 981.
Poids le plus faible et poids le plus fort
Souvent dans les systèmes de numérotation, en électronique numérique et en programmation, nous utilisons les termes "poids le plus faible" et "poids le plus fort", appelés aussi LSB et MSB pour Least significant Bit et Most Significant Bit (terminologie en anglais) pour désigner respectivement les deux chiffres ayant la plus faible valeur positionnelle.
Dans l'exemple précédent, nous notons ainsi que le chiffre 9 représente le chiffre du poids le plus fort et le chiffre 1 représente le chiffre du poids le plus faible. L'image ci-dessous nous explique cela :

Prenons un deuxième exemple, le nombre 3278 dans le système décimal s'écrit \(N=(3278)_{10} \). Ce nombre 3278 est en effet calculé à partir de la formule suivante :
\[N=(3278)_{10} = 3\times 10^{3} + 2 \times 10^{2} + 7 \times 10^{1} + 8 \times 10^{0}\]
Or \(10^{0} = 1\), ce qui nous donnes :
\(N = 3\times 1000 + 2 \times 100 + 7 \times 10 + 8 \times 1\).
N = 3000 + 200 + 70 + 8 = 3278
Ainsi, le chiffre 3 dans ce nombre représente le chiffre dont le poids le plus fort et le chiffre 8 représente le chiffre dont le poids le plus faible. L'image ci-dessous nous démontre cela :

Les entiers, les nombres décimaux
Dans le système de numérotation décimal, une particularité par rapport aux autres systèmes de numérotation (binaire, octal et hexadécimal) a été introduite : la virgule. Ce caractère « , » ajoute à un nombre une valeur fractionnelle inférieure strictement à 0 et supérieure à 0 et inférieure à 1. Ainsi, nous distinguons les nombres décimaux des nombres entiers. Par exemple, la moitié d'une part est représenté dans le système décimal par 0.5 ou \( \frac{1}{2} \), et le quart de part est représenté \( \frac{1}{4} \) ou 0.25.
Pour comprendre le système décimal, il existe diverses méthodes qui peuvent faciliter et aider l'assimilation de ce système décimal à base 10 telles que:
- La méthode des blocs,
- la numération orale
- la numération gestuelle
- La monnaie : pièces et billets.
- etc.
A découvrir aussi, autres systèmes de numérotation
| < Le système de numérotation | L'électronique numérique | Le système binaire > |