Le système octal

Le système octal est un système de numérotation de base 8, ce qui signifie que ce système n'utilise que huit chiffres pour représenter des valeurs numériques dans un système très particulier. À la différence du système décimal (en base 10), qui utilise dix chiffres, le système octal ne prend pas en compte les chiffres 8 et 9. Ainsi, chaque chiffre octal est placé dans une position qui correspond à une puissance de 8, avec 8⁰ qui représente la plus petite valeur qui est égale à 1 (le plus petit chiffre à droite tout à droite du nombre octal).

Par exemple, le nombre octal 133 est l'équivalent de 91 en décimal. Pour le décoder, nous appliquons la formule suivante : \( 1 \times 8^2 + 3 \times 8^1 + 2 \times 8^0 = 64 + 24 + 3 = 91 \)

Le système octal est utilisé assez fréquemment dans les domaines de l'informatique et de la programmation. Dans certains langages de programmation, le système octal permet de représenter de manière plus précise des valeurs binaires, tandis que l'octal a été utilisé dans les anciens systèmes d'exploitation et dans les systèmes embarqués pour modéliser certaines informations, telles que les informations relatives aux tables d'allocation de fichiers, les permissions, etc.

Les opérations et les opérateurs

Dans le système de numérotation octal, les opérations sont semblables à celles du système de numéroation décimal, mais il est important de prendre en compte les règles de retenues et de transfert propres au système octal. Voici un donc les principales opérations:

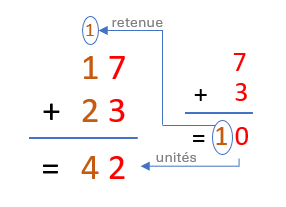
• L'addition: Pour additionner des nombres octaux, on aligne les chiffres en colonne par puissance de 8, comme dans le système décimal. On additionne ensuite colonne par colonne, en tenant compte du fait que si la somme dépasse 7 (puisque 8 n'existe pas dans ce système), il faut la retrancher.

• La soustraction: Pour soustraire deux ou plusieurs nombres décimaux, on applique les mêmes principes que pour la soustraction dans le système décimal, avec la même règle de l'emprunt si la soustraction est impossible..
• La mutltiplication: pour multiplier des nombres dans le système octal, on utilise la même méthode que dans le système décimal, mais en respectant la limite de 8 puisque le chiffre 8 n'existe pas dans ce système. Par exemple, \( 5 \times 5 = 31 \) et non pas \( 25 \).
• La division: nous suivons les mêmes étapes que la division dans le système décimal, mais nous devons faire les calculs dans le système en base 8. Le résultat de la division donne également un quotient et un reste.

Ainsi, les principes fondamentaux de ces opérations demeurent identiques à ceux du système décimal, mais il est essentiel de faire attention à nos calculs, car nous sommes dans un système en base 8.

Pour ce qui est des opérateurs, nous pouvons citer les opérateurs de comparaison utilisés pour comparer des nombres octaux, tels que :

• Supérieur (>), supérieur ou égal (≥): pour indiquer que le premier nombre est plus grand que le deuxième. Par exemple, 37 > 26.
• Inférieur (<), supérieur ou égal (≤): utilisé pour indiquer que le premier nombre est plus petit que le deuxième. Par exemple 31 ≤ 127.
• Egal: cet opérateur est utilisé pour tester si les deux nombres sont égaux.
• Différent: cet opérateur est utilisé pour tester si les deux nombres sont différents.

Ces deux derniers opérateurs sont utilisés assez souvent dans l'algorithmique et la programmation pour la comparaison de deux variables dans le système octal.