Exercices - Calcul de l'inductance équivalente

Exercice 1 : inductance montées en série

Pour le montage des trois inductances ci-dessous montées en série, calculez la valeur de l'inductance équivalente \( L_{eq} \) entre les deux points A et B :

Schéma de trois inductances montées en série

Pour les deux valeurs suivantes de :

\(L_{1} \) = 100 mH
\(L_{2} \) = 220 mH
\(L_{3} \) = 300 mH

Exercice 2 : inductances montées en parallèle

Pour le montage des quatre bobines ci-dessous montées en parallèle, calculez la valeur de l'inductance équivalente \( L_{eq} \) entre les deux points A et B :

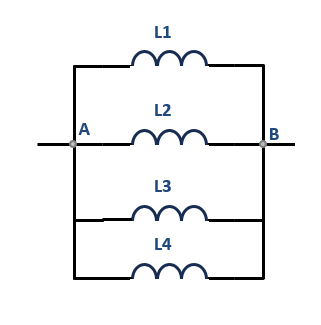
Schéma de quatre inductances montées en parallèle

Pour les deux valeurs suivantes de :

\(L_{1} \) = 50 mH
\(L_{2} \) = 100 mH
\(L_{3} \) = 250 mH
\(L_{4} \) = 150 mH

Exercice 3 : inductances en montage mixte 1

Pour le schéma ci-dessous, déterminez la valeur de l'inductance équivalente \( L_{eq} \) entre les deux points A et C :

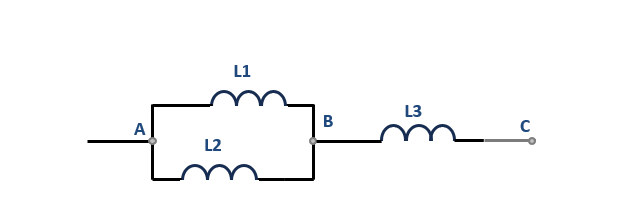
Schéma de plusieurs inductances (appelées aussi bobines) montées en montage mixte

Pour les valeurs suivantes de :

\(L_{1} \) = 150 mH
\(L_{2} \) = 330 mH
\(L_{3} \) = 780 mH
\(L_{4} \) = 120 mH